Quarantine Logs 2020-04-13: Circuit-Sim Progress!

Been a week! This is by far the most frequently I’ve ever posted. I’m hoping to keep it up.

I’m happy to update that I made a little progress on the circuit simulator I’ve been working on. Here I’ll get into some of what that’s all about in a little bit more detail. All the relevant code is up on Github, though it’s really bare-bones and without documentation as of the time of writing.

Learning about circuit analysis introduced me to the concept of nodes. A node is a point in a circuit where two or more components meet. This concept is important because of Kirchhoff’s Current Law, which states that the sum of currents leaving a node is 0.

$$ \text{Current leaving node $i$} = \sum_{j \in N(i)} I_{i,j} = 0 $$

Here’s an example:

Note that this system can also be solved by the matrix equation

$$ \begin{bmatrix} 1 & 0 & 0 & 0 \\
-1/R_1 & 1/R_1 + 1/R_3 + 1/R_2 & -1/R_3 & -1/R_2 \\
0 & -1/R_3 & 1/R_3 + 1/R_4 & -1/R_4 \\
0 & 0 & 0 & 1 \\
\end{bmatrix} \begin{bmatrix} V_s \\ V_1 \\ V_2 \\ V_{\text{GND}} \end{bmatrix} = \begin{bmatrix} V_s \\ 0 \\ 0 \\ 0 \end{bmatrix} $$

There’s a bit of abuse of notation here with \( V_s \) referring both to the variable corresponding to the voltage level at the voltage source, and the value of the voltage it adds.

When we consider a circuit with only resistors, the current leaving the node from each branch is equal to the voltage drop along the resistor divided by its resistance. (Ohm’s Law states that \(V = IR\)). Thus, if \(N(i)\) refers to the set of nodes that are adjacent to node \(i\), we have

$$ \text{Current leaving node $i$} = \sum_{j \in N(i)} \frac{V_i - V_j}{R_{i,j}} = 0$$

At this point I practiced with a couple of circuits, calculating the voltage level at each node by hand, eventually moving onto just solving for the voltage level at each point by solving a linear system via matrices. After a couple of these I started to notice that all of this started to look a little familiar. That’s right—this looks a lot like a “graph kind of computation” would fit perfectly. The “nodes” in the circuit are just the same as “nodes” in a graph, and the resistors are just like a graph’s edges, storing information. Given the properties of circuits, I determined that the best thing to work with here are undirected graphs, with the possibility of having multiple edges between any two nodes; this is certainly possible in a circuit.

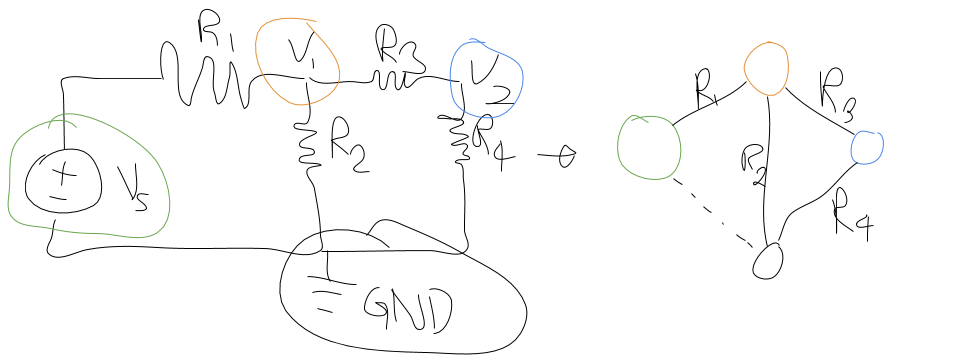
It turns out that that’s almost enough to start implementing a circuit simulator! You take your graph representation of your circuit, and run it through some function that will generate a linear system for that graph. Once you have that you can automatically solve the linear system to find the voltages at every single node. It’s still pretty early so I currently support circuits that have exactly one voltage source and where the only type of circuit component is a resistor.

I chose Julia to implement it, mostly because its matrix solving syntax is nice.

Here’s my circuit representation. A Node (which I’ve left out the implementation of) can either be a VoltageSource (adding a set amount of voltage) or a BaseNode, which is just a wire junction.

mutable struct Circuit
    ground::Node
    nodes::Dict{String, Node}
    edges::Array{Edge}

    function Circuit()
        ground = BaseNode()
        nodes = Dict()
        get!(nodes, "GND", ground)
        edges = []
        return new(ground, nodes, edges)
    end
end

And here’s my current version of solve_voltages. To generate the linear system I follow a couple of basic rules:

using LinearAlgebra

# ...

function update_soln_matx!(S::Array{T, 2}, c, i, j, node1, node2, R) where {T <: Real}
    if !isa(node1, VoltageSource) && node1 != c.ground
        S[i, i] += 1 / R
        S[i, j] += -1 / R
    end
end

function solve_voltages(c::Circuit)
    names = [n[1] for n in collect(c.nodes)]
    node_to_idx = Dict([name => i for (i, name) in enumerate(names)])
    N = length(c.nodes)
    S = zeros(N, N)
    b = zeros(N, 1)

    z = node_to_idx["GND"]
    S[z,z] = 1

    for (name, node) in c.nodes
        if node isa VoltageSource
            i = node_to_idx[name]
            S[i, i] = 1
            b[i] = node.added_voltage
        end
    end

    for (name1, name2, con) in c.edges
        node1 = c.nodes[name1]
        node2 = c.nodes[name2]
        i = node_to_idx[name1]
        j = node_to_idx[name2]
        if con isa Resistor
            R = con.resistance
            update_soln_matx!(S, c, i, j, node1, node2, R)
            update_soln_matx!(S, c, j, i, node2, node1, R)
        else
            throw(MethodError("Only resistors supported at this time."))
        end
    end

    if DEBUG
        println(S)
        println(b)
    end
    return inv(S) * b
end

Here’s a couple of examples:

# Really basic case with two resistors.
c = Circuit()
register_node!(c, "n1", VoltageSource(5.0))
register_node!(c, "n2", BaseNode())
connect_nodes!(c, "n1", "n2", Resistor(5.0))
connect_nodes!(c, "n2", "GND", Resistor(10.0))
println(solve_voltages(c))
# output: [5; 3.3333; 0]

# This one is equivalent to the diagram at the top of the post with some
# arbitrary values chosen for resistances.
c2 = Circuit()
register_node!(c2, "n1", VoltageSource(12.0))
register_node!(c2, "n2", BaseNode())
register_node!(c2, "n3", BaseNode())
connect_nodes!(c2, "n1", "n2", Resistor(4000.))
connect_nodes!(c2, "n2", "n3", Resistor(2000.))
connect_nodes!(c2, "n2", "GND", Resistor(1000.))
connect_nodes!(c2, "n3", "GND", Resistor(2000.))
println(solve_voltages(c2))
#output: [12; 2.0; 1.0; 0]

So that’s where I’m at so far! There are some pretty natural extensions to what I’ve done so far:

If you’re interested in learning more about circuit analysis, the book I’ve been going through is Electric Circuits by James S. Kang. It offers a really concise introduction to circuit analysis and has tons of exercises to practice with.